宇宙学质疑
——评狭义相对论的时空观和哈勃定律
周君毅
版权所有,未经许可不得转载、出版、印刷、发表.
欢迎各出版商 联系合作 出版
内容提要
本书有两部分内容:第一篇(含笫1、2章)评论狹义相对论的时空观;第二篇(笫3章)评论哈勃定律。
在笫一篇中作者认为狹义相对论对绝对空间的否定是错误的,所提出的光速不变原理也是错误的。绝对空间客观存在,是否定不了的。宇宙中的所有物质作为一个统一体在靜态空间中运动、演变。在这个统一体中我们可以确立一个三维中心坐标系。在这个坐标系中所有的物质具有统一的时间,一个物质点在任何时刻都有确定的坐标位置。它不会因为该物质点运动的快慢而改变,也不会因为观測者运动的快慢而改变。作者提出与狹义相对论完全对立的统一论:统一的物质体系,统一的坐标系,统一的时间。
在笫二篇中作者指出1929年美国天文学家哈勃成功地发现河外星系的光谱红移与它们到地球的距离成正比。但是却错误地认为产生谱线红移的原因是多普勒效应。作者认为产生谱线红移的主要原因是光波(光子)在长时间的传播过程中能量的自然衰减。
目 录
第一篇 评狭义相对论的时空观………………………………………………1
第一章 宇宙、空间、物质……………………………………………………1
1.1 两种宇宙观…………………………………………………………………1
1.2 宇宙是有限的,还是无限的?……………………………………………2
1.3 宇宙有无中心………………………………………………………………3
1.4 物质体系的中心坐标系……………………………………………………4
第二章 时间与光速……………………………………………………………6
2.1 物质体系的统一时间………………………………………………………6
2.2 双生子佯谬…………………………………………………………………6
2.3 同向运动体之间的光传播问题……………………………………………7
2.4 同时的相对性………………………………………………………………9
2.5 洛仑兹速度转换和伽俐略转换……………………………………………10
2.6 光速不变原理………………………………………………………………12
2.7 迈克耳逊——莫雷实验……………………………………………………13
第一篇结束语……………………………………………………………………17
第二篇 评哈勃定律……………………………………………………………19
第三章 评哈勃定律……………………………………………………………19
3.1 光谱线红移和哈勃定律……………………………………………………19
3.2 问题…………………………………………………………………………19
3.3 什么情况下视线速度能与距离成正比?…………………………………20
3.4 星系均衡扩散的三维球面模型……………………………………………21
3.5 谱线红移的其它解释………………………………………………………23
3.6 产生红移的原因是光子能量的衰减………………………………………25
第二篇结束语……………………………………………………………………26
第一篇 评狭义相对论的时空观
第一章 宇宙、空间、物质
1.1 两种宇宙观
承认或是不承认绝对空间的存在,宇宙是有限的、还是无限的,宇宙有无中心等问题,一直是宇宙学争论的问题。
古人称:“往古来今谓之宙,四方上下谓之宇。”即宇为空间,宙为时间。现代通常把空间、时间及空间所容纳的物质联系在一起,把太空的一切统称为宇宙。
近代有两种不同的宇宙观,一种是牛顿的绝对时空观。他把时间看成独立于物质的,不断流逝的长河。把空间看成独立于物质的永远不变的装载物体的容器。把物体的运动看成是在绝对空间中的位置变化。牛顿的时空观承认绝对空间的存在,且认为空间的所有物质(可称为物质体系或物质世界)包容于其中,并在其中运动。受历史条件的限制,牛顿的理论难免有不足之处。但是,我们认为他的基本观点仍是正确的,关于时间,我们将在后面阐述,本章将讨论空间和物质方面的问题。
另一种宇宙观是爱因斯坦根据相对论提出的“静态、有限、无界”的宇宙模型。他否定绝对的时空。后来弗里德曼等人提出了大爆炸宇宙论,以动态的宇宙膨胀理论否定了过去的静态宇宙模型。但是,在是否存在绝对时空的问题,依然是爱因斯坦的相对论占据主导地位。
在《相对论的意义》(阿尔伯特·爱因斯坦著,上海科学教育出版社,2003年1月第1版)一书中,爱因斯坦谈到了空间的概念。“将物体B、C……附加到物体A上去,可以形成新的物体,我们说我们延伸了物体A。我们可以这样延伸物体A,使其与任意其他物体相接触。物体A的所有延伸的集合,我们可以定义为‘物体A的空间’。于是一切物体都在(随意选定的)物体A的空间的说法是正确的。在这种意义下,我们不能抽象地谈论空间,而只能谈论属于物体A的空间。”爱因斯坦讲的空间是物体A的延伸,以物体A为中心的物体的集合,称属于物体A的空间,也就是随物体A一起运动的空间。不是那种什么都没有的静态空间。
爱因斯坦还指出:“不存在空虚空间这种东西,即不存在没有场的空间。空间——时间本身并没有要求存在的权利,它只是场的一种结构性质。”他说:“我们今天的世界图象就得承认有两种概念彼此完全独立的(尽管在因果关系上是相互联系的)实在,即引力场和电磁场,或者——人们还可以把它们叫做——空间和物质”。(引自《爱因斯坦是怎样创建相对论的》,尤广建著,湖南教育出版社,1999年4月第1版第4次印刷)。在这里,物质的又一种延伸——引力场和电磁场被爱因斯坦称为空间。
在《科学的丰碑——20世纪重大科技成就纵览》(陈建礼主编,山东科学技术出版社,1998年12月第1版第1次印刷)一书中,明确指出:“同任何外界事物都不发生联系的,任何实验都无法观察和检测出来的,实际上根本不存的绝对时间、绝对空间和绝对运动的概念和理论,作为某个历史时代人类认识自然的最优秀的成就,随着20世纪晨曦曙光的冉冉闪耀,永远地被请进了人类文明的历史博物馆。”
爱因斯坦说不存在空虚空间这种东西,《科学的丰碑》说根本不存在绝对时间、绝对空间和绝对运动的概念和理论,并说这些东西永远被请进了人类文明的历史博物馆。但是,有些话说得也许太武断了。爱因斯坦提出相对论已经一百年了,人们依然没有忘记绝对时间、绝对空间、绝对运动的概念和理论。任何物质都容纳在广阔的、无边无际的空间之中,怎么能说空间同任何外界事物都不发生联系呢?任何物质(事物)都包容于空间内,并在其中作各种各样的运动,有目共睹,还要如何观察和检测呢?空间的本质就是什么都没有的真空,如果真能像检测实物一样检测出来的话,那就不叫空间了,空间是客观存在的,请不要说它“实际上根本不存在”,也不需要任何人赋予它存在的权利。
爱因斯坦定义的空间并非真正的空间,它只是物体(不管是实物,还是引力场或电磁场)的延伸。空间包容了宇宙中所有的物质,但不能说成属于物体A或属于物体B的空间。说“不存在没有场的空间”,把空间和时间看成“只是场的一种结构性质”,这只能说明爱因斯坦时空观的偏执。场同实物一样存在于空间之中,但不能把空间和时间一起看成“只是场的一种结构性质”。同实物一样,场是有限的。一个星系的引力场、电磁场无论多么强大,同无限的空间相比,它的作用范围是极小的。有限的场怎么能同无限的空间混为一堂?当主体星系演变和运动时,场也随之变化和运动,而我们所定义的空间是静态的,永恒的。动态的场和静态的空间是两个不同的概念,场取代不了空间。
爱因斯坦否定绝对空间,并将空间的概念和物质(物体A、B……或引力场、电磁场等)混同在一起。我们承认绝对空间,也就需要把空间同物质予以分开。报刊、杂志、书籍中有关宇宙的概念常常是模糊的,不能区分物质和空间。例如,人们常说的宇宙膨胀,往往指的是空间和物质一起膨胀,实际上只是物质由空间的一个小范围开始,向四周的扩散,静态的空间并不随物质扩散。
1.2 宇宙是有限的,还是无限的?
明确绝对空间的概念,并区分物质和空间,我们就可以讨论宇宙是有限的,还是无限的,宇宙有无中心等问题了。
爱因斯坦认为宇宙是“有限、无界的”。但是,从数学的观点看,限和界的概念是相关的。有限应有界,数量有限的物质分布的范围应该是有限的。爱因斯坦的“有限、无界”论不能让人信服。他解释不了这个问题,因为他否定绝对空间的存在,不能把物质和空间分开。
当我们把物质和空间分开后,这个问题的解答非常简单:宇宙中的物质体系是有限的,空间则是无限的。有限的物质存在于无限的空间之中,并在其中演变、运动。同宇宙膨胀的概念一样,不把物质和空间分开是得不到正确的答案的。只有抛开宇宙这个模糊的概念,把物质和空间分开,才能得到有限的物质体系和无限的空间的正确答案。
1.3 宇宙有无中心?
既然物质体系是有限的,那么它必定会有一个中心。这里所讲的中心不是宇宙的中心,更不是空间的中心,而是物质体系的中心。
1999年10月24日的《参考消息》刊登了一篇署名为美国能源部的短文,标题为《问:宇宙有中心吗?》。该文说,“简单地回答,宇宙没有中心。我们常说宇宙中各个星系正远离我们而去,许多人便误以为我们处于宇宙的中心。请记住宇宙是均质和各向同性的,无论从宇宙中的任何一个点观察,向四周看上去,都是一样的。……有人觉得这种解释难以理解,那么可以用球体的表面来解释这个问题。你能说球体表面的任何一个点是中心吗?当然不能。宇宙也是同样的道理,宇宙自诞生以后,一直向外膨胀。但是我们不能说宇宙是从某一个特定的点向外膨胀的。”
作为权威性的美国能源部的这种宇宙无中心论代表了主流科学界的观点,也是爱因斯坦的观点,影响已久。这篇短文文字不多,却阐述了宇宙无中心论的主要观点。
说宇宙是均质和各向同性的,应该指宇宙中物质的分布是均匀的和各向同性的。如果物质体系是静态的,这种均质和各向同性的说法尚有可能。如果物质体系是动态扩散的,这种均质和各向同性的说法显然错了。根据宇宙大爆炸理论,宇宙中的物质长期向外扩散,这种动态分布的物质体系难以维持在各处的均匀分布——除非每一个单位体积内的物质都是均匀扩散的。在物质不断向外扩散的时候,各处的物质在扩散方向、扩散的反方向、以及这两个方向之外的其它方向的运动特征都不会一样,也不会有各向同性。认为从宇宙中的任何一个点向四周观察都是一样的,是没有根据的,在宇宙中的不同位置观察四周的物质将不会是相同的。
有中心论者并没有像古人一样,认为我们(地球、太阳或银河系)处于宇宙的中心。所谓“误认为”只是该文自己的误以为。反过来,倒是无中心论者常常以自己的观察点为中心。
该文说“球体表面的任何一个点不会是宇宙的中心”。却不愿意告诉读者,球体或球面有一个中心,那就是球心!该文承认宇宙膨胀(物质体系向外扩张)理论,却否定宇宙是从某个特定的点向外膨胀的,而这个特定的膨胀起点又可能正好是球体或球面的中心。如果大爆炸宇宙起源理论是正确的,宇宙是由最初的一点爆炸形成的,即物质体系是由一点开始扩散的,这最初的一点就应该是它的中心。如果物质体系是呈球面形态,各个方向均衡向外扩散的,那么,扩散球面的中心,即扩散的起点,就是物质体系的中心。如果物质体系向外扩散时,各个方向的速度不是均衡的,即扩散时并非球面形态,扩散的起点依然是物质体系的中心。即使大爆炸理论是错误的,有限的物质体系也一定会有一个质量中心。
需要重申的是:这里所说的中心是物质世界或称物质体系的中心,它也可以视为宇宙的中心。但是说物质世界或物质体系的中心更确切。说成宇宙的中心,有时会误以为是宇宙空间的中心。空间是真空,是无限的,它各处一样,没有中心。有限的物质体系必定有一中心,按照扩散理论,扩散的起点应该就是该中心。有人用所谓的“奇点”,否定扩散起点的存在,这是错误的。物质体系有一个实实在在的中心点,不是虚无的奇点。
这个点在什么位置呢?如果宇宙膨胀理论是正确的,我们只要沿着星系扩散的反方向,即可以找到这个点。在天体观测日益发展的今天,这应该是可以做到的。如果宇宙膨胀理论是错误的,未来通过更精细的天文观测和计算,也总可以找到这个中心点。
1.4 物质体系的中心坐标系
一旦确定了物质体系的中心,我们即可以以它为原点建立三维坐标系。这个坐标系可称为物质体系的中心坐标系或统一坐标系。为了便于计算,我们研究地球时,取地心为坐标系中心,研究太阳系时,取太阳为坐标系中心,研究银河系时,取银心为坐标系中心。同样道理,研究整个物质体系时,也应该取其中心建立坐标系。
中心坐标系的建立,不仅方便了对整个物质体系的研究,同时也对爱因斯坦的狭义相对论提出了极大的挑战。相对论者否定宇宙有中心,也就是否定中心坐标系。他们认为“无论从宇宙中的任何一点观察,向四周看上去,都是一样的。”然而,按照狭义相对论的理论,对同一事物的观察将因处于不同的惯性系而不同。不同的惯性系会因运动速度的不同,产生时间和距离方面的差异,当惯性系运动速度较大时,时间会变慢,距离会缩短。因此,从宇宙中不同的点(不同的惯性系)观察宇宙时,结果将不一样。
我们认为宇宙中的整个物体系有一确定的中心,并且能够在该中心建立一个统一的中心坐标系,将整个物质体系全部涵盖于其中。因而,在物质体系中的任何一个物质点发生的任何事件将有确定的(唯一的)统一坐标系时间(统一时间),它不会因观测者处于不同的位置,或不同的运动状态而变化。同样,在某一时刻,中心坐标系内的每一个物质点都将有确定的坐标。任意两个物质点之间的距离将是确定的(唯一的),它不会因观测者不同而变化。当我们向4光年距离的一个天体发射飞船时,其速度接近光速,到达时间为4年;如果它的速度为光速的百分之一,到达时间为400年;如果它的速度为光速的万分之一时,到达时间则为4万年。这个4光年的距离不会因飞行的速度而改变。在接近光速飞行时,按照狭义相对论的理论,飞船上的时钟要走得慢些。但从统一时间看,从出发至到达依然是4年。
只有把宇宙中所有的物质看做一个整体,并在其中建立一个统一的三维坐标系,我们才能清晰地标定整个物质体系,确定各个星体在空间的位置和运动状态。无中心论认为从宇宙中任何一点向四周观察都是一样的,说明他们对宇宙中的物质体系缺乏整体认识。从某一个点(如地球)观测宇宙,将所得到的各星体的空间位置数据,通过一定的数学转换,可以得到中心坐标系中的宇宙星体分布和运动规律图。但中心坐标系中的宇宙星体分布图同某一点的星体观测图是有区别的,只有中心坐标系下的宇宙星体分布图才能最简明地表明宇宙中各星体的位置和运动状况。以太阳系为例,我们通过在地球上的观测,得到以太阳为中心的太阳系行星运动图,从而简明地反映出太阳系中行星的运动状况。地球或火星对太阳系的观测图无法与之相比。
但是由于现代天文观测的局限性,我们对整个物质体系的了解还很少,还不能确定宇宙中物质体系的分布情况和运动情况,还不能确定物质体系的中心位置,无法建立物质体系的中心坐标系。
目前,我们只能在地球上对宇宙进行观测,寻找物质体系在空间的分布规律和运动规律。我们只能建立以地球为原点的三维坐标系,标定物质体系。一旦确定了整个物质体系的物质分布规律和运动规律,确定了整个物质体系的中心位置,可以通过一定的数学转换,将以地球为原点的三维坐标系下的物质体系物质分布和运动规律图变为以物质体系中心为原点的三维坐标系下的物质分布和运动规律图。这就像我们从地球观测太阳系一样,由地球观测到的太阳系星体分布、运动规律图,可以转换为以太阳为中心的太阳系星体运动规律图。先建立以地球为原点的三维坐标系,对物质体系进行观测,并非像无中心论所言,是以地球为中心。我们要(只有)通过在地球上的观测,得到物质体系的物质分布和运动情况的数据,再通过数学关系转换为以物质体系中心为坐标原点的三维坐标系下的物质体系中物质的分布和运动规律,这与无中心论所说的以地球为中心是两回事。
以地球为原点的三维坐标系中的物质分布情况和运动特征同以物质体系中心为坐标原点的中心坐标系中的物质分布情况和运动特征是不一样的。但它们之间存在一定的数学转换关系。这种转换如同把地球观测到的太阳系星体的运动规律转换为以太阳为中心的太阳系星体的运动规律。整个物质体系具有统一的时间,我们这里讲的只是三维坐标系下的转换,因此这种转换不会有狭义相对论所谓的“动钟延续”、“动尺缩短”。
最后,我们想谈一下,物质体系的中心坐标系和绝对空间的关系。该坐标系在绝对空间中是静态的,还是运动的?如果是运动的,那又是作什么运动?这一些都只能留待未来的天文观测分析解决。
第二章 时间与光速
2.1 物质体系的统一时间
当我们把整个物质体系看成一个整体,并在其中建立一个中心坐标系时,物质体系中的各个物质点将有确定的坐标位置,具有统一的时间。即使我们目前无法确定物质体系的中心位置,无法建立中心坐标系,但这并不影响我们把整个物质体系看成一个整体,确定这个整体具有的统一时间。如果宇宙大爆炸理论是正确的,那么从大爆炸一刻诞生整个物质体系起,到宇宙中的物质体系演变到目前的形态,整个物质体系中的所有物质经历的是同一时间。该时间若是150亿年,那么宇宙中的所有物质都是150亿年,不会因任何原因(包括运动速度)而有所差异。不能说有些物质经历了140亿年,或有些物质经历了160亿年。
狭义相对论者认为:时间像河流,有些地方流得快一些,有些地方则流得慢一些。他们提出时间隧道和“虫洞”等概念,幻想能超越时空,回到从前或进到未来。但这些终归只是无法实现的幻想,甚至可以说是对青年的误导。
在洛仑兹转换中,一个过程,发生在不同惯性系的同一地点,则相对静止的惯性系测量到过程的时间间隔数值最小,即过程的时间间隔最短,称为该过程的固有时间,记作 ![]() 。其它所有相对该惯性系运动的惯性系测量该过程的时间间隔数值都大于固有时间,记作
。其它所有相对该惯性系运动的惯性系测量该过程的时间间隔数值都大于固有时间,记作 ![]() 。则有
。则有
![]()
其中:c为光速, ![]() 为两个惯性系之间的相对速度。
为两个惯性系之间的相对速度。
该式称为狭义相对论的运动时钟变慢。
为了验证这个理论,人们进行了各种实验,如测量飞机、卫星上的时钟与地面上时钟的差异。由于飞机与卫星的运动速度不是很快,处于加速或失重状态下的时钟与地面上的时钟难免有差异,这方面的精确性难以让人信服。
行星绕着太阳运动,行星上的时钟是否比太阳的时间走得慢呢?不会的,太阳系演变到现在,行星和太阳具有同一时间标准。
2.2 双生子佯谬
狭义相对论缺乏整个物质体系的概念。前面提到:“在相对静止的惯性系测量到一个过程的时间间隔数值最小,称为该过程的固有时间。”这种叙述是近来的提法,狭义相对论中洛仑兹转换相关的两个惯性系只有相对速度的概念,并没有相对静止的概念。两个惯性系要确定谁相对静止,必须要有第三者参照。而且这个第三者还必须和整个物质体系或静态空间相联系,才能确定其本身运动的快慢,才能作为参照物,判断两个惯性系中谁相对静止。过去说的时间延缓,指甲惯性系上观察乙惯性系上的时间相对慢了;乙惯性系上观察甲惯性系上的时间相对慢了,并不是说运动快的惯性系上的时间比运动慢的惯性系上的时间延缓了。
因此,历史上就因时间延缓的相对性,引出了“双生子佯谬”。孪生兄弟甲留在地球上,乙乘高速飞船远航返回地球。根据洛仑兹转换的时间延缓效应:在甲看来,乘飞船返回的乙比甲自己年轻;而在乙看来,留在地球上的甲比自己年轻。究竟谁较年轻,洛仑兹转换回答不了这个问题,称双生子佯谬。请注意,这里的“在甲看来”,即乙相对甲;“在乙看来”即甲相对于乙,二者之间的相对速度为高速。但是,这里只提到二者的相对速度为高速,并没有讲:谁的绝对速度较低,即谁“相对静止”。
只是在后来,才提出了“相对静止”的问题。而一旦提出“相对静止的概念”,就必须确立物质体系的整体概念。缺乏整体概念,就不能确定两个惯性系中谁运动得较快,谁运动得较慢(相对静止)。在茫茫的宇宙中,两个星体擦肩而过,如果不考虑周围的环境,你能指出谁相对静止吗?所谓的“相对静止的惯性系”的提法,似乎只是两个惯性系之间的问题,实际上却超出了两个惯性系的范围。
为了避免出现“双生子佯谬”,“动钟延缓”引入了“相对静止的惯性系”概念。而“相对静止”又让狭义相对论陷入了新的矛盾。如何确定洛仑兹转换的两个惯性系中,哪一个是“相对静止的惯性系”呢?
2.3 同向运动体之间的光传播问题
在科普书中有如下的一个例子,用以阐述动钟的延缓,简述如下:
飞机A和B以等速 ![]() 同向平行飞行,见图2.3-1,A、B连线与飞行方向垂直。由A机向B机发射雷达波,探测与B机的距离。设固连于飞机A的坐标系为
同向平行飞行,见图2.3-1,A、B连线与飞行方向垂直。由A机向B机发射雷达波,探测与B机的距离。设固连于飞机A的坐标系为 ![]() ,固连于地面的坐标系为
,固连于地面的坐标系为 ![]() 系。
系。 ![]() 系的标准钟为
系的标准钟为 ![]() ,
, ![]() 系的标准钟为
系的标准钟为 ![]() 。
。
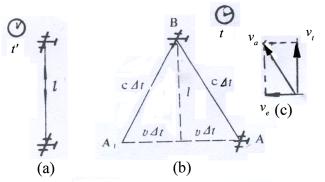
图2.3-1
雷达信号的往返路径在 ![]() 系和
系和 ![]() 系是不同的,如图2.3-1所示。在竖直方向s系和
系是不同的,如图2.3-1所示。在竖直方向s系和 ![]() 没有相对运动,可以认为在竖直方向上的距离是相同的,如图2.3-1(a)所示,
没有相对运动,可以认为在竖直方向上的距离是相同的,如图2.3-1(a)所示, ![]() 。
。
把雷达信号自A机发出到达B机称为第一事件,把雷达信号到达B机后反射回A机称为第二事件。钟 ![]() 指示的这两个事件的时间间隔为
指示的这两个事件的时间间隔为 ![]() ,钟
,钟 ![]() 指示的时间间隔为2
指示的时间间隔为2 ![]() 。由于光速各向同性,雷达信号“往”和“返”所经历的时间是相等的。
。由于光速各向同性,雷达信号“往”和“返”所经历的时间是相等的。
由图2.3-1(a)可知
![]() (2.3-1)
(2.3-1)
其中 ![]() 为雷达波传播速度
为雷达波传播速度
由图2.3-1(b)可知雷达信号的路径是一个等腰三解形ABA1的两腰,而A机的飞行路径是这个三角形的底边。
腰长为 AB=c ![]() (2.3-2)
(2.3-2)
底边长为 AA1=2v ![]() (2.3-3)
(2.3-3)
由几何关系可确定 ![]()
即 ![]() (2.3-4)
(2.3-4)
把式(2.3-1)代入式(2.3-4) 得
![]()
即 ![]()
或 ![]() (2.3-5)
(2.3-5)
因为 ![]() <1
<1
因此 ![]() <
< ![]()
即动钟慢了。
上面的论述有什么问题呢?问题出在“光速不变的原理”。作者认为在动系 ![]() 上雷达信号传播的速度为
上雷达信号传播的速度为 ![]() ,有
,有 ![]() ,这是错误的。这是一个典型的伽俐略速度矢量合成的问题。雷达信号沿等腰三角形
,这是错误的。这是一个典型的伽俐略速度矢量合成的问题。雷达信号沿等腰三角形 ![]() 的腰AB方向的速度为
的腰AB方向的速度为 ![]() ,是绝对速度,以
,是绝对速度,以 ![]() 表示。飞机A的运动速度
表示。飞机A的运动速度 ![]() 为牵连速度,以
为牵连速度,以 ![]() 表示。雷达信号在动系
表示。雷达信号在动系 ![]() 系的速度是相对速度,以
系的速度是相对速度,以 ![]() 表示,见图2.3-1(c)。由矢量合成关系。
表示,见图2.3-1(c)。由矢量合成关系。
![]() =
= ![]() +
+ ![]()
即 ![]()
![]() (2.3-6)
(2.3-6)
上式表示,雷达信号在 ![]() 系中的相对速度不是
系中的相对速度不是 ![]() ,而是
,而是 ![]() 。
。
因此, ![]()
![]()
![]()
![]()
结果,在第一事件中,动钟和静钟的时间相同。同样的道理,在第二事件,动钟和静钟的时间也会相同。
两种计算,两种结果,问题就在雷达信号在 ![]() 系中是否为光速?雷达信号传播的真实路径是等腰
系中是否为光速?雷达信号传播的真实路径是等腰 ![]() 的腰AB斜线,而不是与运动方向垂直的
的腰AB斜线,而不是与运动方向垂直的 ![]() 方向。AB方向为光速,而在
方向。AB方向为光速,而在 ![]() 方向雷达信号在
方向雷达信号在 ![]() 系中的相对速度并不是光速。它只是光速矢量的一个分矢量,大小为
系中的相对速度并不是光速。它只是光速矢量的一个分矢量,大小为 ![]() 。
。
类似的例题在多本高校物理教材中出现。如列车在行进时,车顶的灯光向地板照射,放在列车上的钟,将测量到光线由车顶传到地板时,时间延缓了。在这些类似的例题中,都是光速不变原理的错误,导致了另一个错误:动钟延缓。
2.4 同时的相对性
同时的相对性是狭义相对论的一个重要命题,相对论常用“爱因斯坦列车”阐述这个问题。
设想有一车厢相对地面以速度 ![]() 作匀速直线运动,在车厢的正中位置有一闪光灯发出光信号,同时向车厢前后两端射去,如图2.4-1所示。
作匀速直线运动,在车厢的正中位置有一闪光灯发出光信号,同时向车厢前后两端射去,如图2.4-1所示。
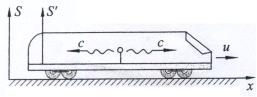
图2.4-1
设地面为 ![]() 系,车厢为
系,车厢为 ![]() 系,光信号到达前壁为事件
系,光信号到达前壁为事件 ![]() ,到达后壁为事件
,到达后壁为事件 ![]() 。对
。对 ![]() 来说,光传向前、后的速度均为
来说,光传向前、后的速度均为 ![]() ,因此光信号将同时到达前后壁,即
,因此光信号将同时到达前后壁,即 ![]() 和
和 ![]() 是同时事件。而对
是同时事件。而对 ![]() 系来说,按光速不变原理,光传向前后的速度也都为
系来说,按光速不变原理,光传向前后的速度也都为 ![]() 。但因车厢以速度
。但因车厢以速度 ![]() 相对
相对 ![]() 系向前运动,所以在
系向前运动,所以在 ![]() 系中观测到光相对于后壁的速度为
系中观测到光相对于后壁的速度为 ![]() ,而相对于前壁的速度为
,而相对于前壁的速度为 ![]() 。因而
。因而 ![]() 系的结论是:光信号到达后壁要比到达前壁早。于是在
系的结论是:光信号到达后壁要比到达前壁早。于是在 ![]() 系中不同地点同时发生的两个事件,在
系中不同地点同时发生的两个事件,在 ![]() 系中观测却不是同时发生的,这说明“同时”具有相对性。
系中观测却不是同时发生的,这说明“同时”具有相对性。
这种阐述讲了一百年了,尽管遭到许多学者的批评,但我们的物理教材中,却从来只讲授“同时的相对性”,而不提人们对它的批评。
在分析“同时的相对性”的错误之前,我们设想一下:如果在爱因斯坦车厢中,由中间位置向前、后同时发射的不是光,而是速度为 ![]() 的的手枪子弹,情况会怎样呢?
的的手枪子弹,情况会怎样呢?
在 ![]() 系,因为子弹具有惯性,向前的子弹速度为
系,因为子弹具有惯性,向前的子弹速度为 ![]() ,向后的子弹速度为
,向后的子弹速度为 ![]() 。因车厢向前以速度
。因车厢向前以速度 ![]() 运动,射向前方的子弹和车厢的相对速度为:
运动,射向前方的子弹和车厢的相对速度为: ![]() 。射向后方的子弹与车厢的相对速度为:
。射向后方的子弹与车厢的相对速度为: ![]() 。两者相同,子弹同时击中前壁和后壁。在
。两者相同,子弹同时击中前壁和后壁。在 ![]() 系射向前、后方的子弹速度均为
系射向前、后方的子弹速度均为 ![]() ,也是同时。
,也是同时。 ![]() 和
和 ![]() 两个事件,不管是
两个事件,不管是 ![]() 系还是
系还是 ![]() 系,都是同时的,并不存在“同时的相对性”问题。
系,都是同时的,并不存在“同时的相对性”问题。
在 ![]() 系中,因为子弹具有一个与车厢速度相同的惯性速度(子弹的速度与发射体的速度有关)致使射向前后的子弹速度不相同,但却同时到达前后壁。在
系中,因为子弹具有一个与车厢速度相同的惯性速度(子弹的速度与发射体的速度有关)致使射向前后的子弹速度不相同,但却同时到达前后壁。在 ![]() 系中,射向前后的子弹速度是相同的,也同时到达前后壁。子弹射向前后壁的“同时”在
系中,射向前后的子弹速度是相同的,也同时到达前后壁。子弹射向前后壁的“同时”在 ![]() 系和
系和 ![]() 系是统一的。
系是统一的。
在爱因斯坦车厢中,射向前后的光信号,因为在 ![]() 系和
系和 ![]() 系中速度相同(都是
系中速度相同(都是 ![]() ),导致射到前后壁的时间在
),导致射到前后壁的时间在 ![]() 系中是不相同的,在
系中是不相同的,在 ![]() 系中却是相同的。问题又出在“光速不变原理”。光在
系中却是相同的。问题又出在“光速不变原理”。光在 ![]() 系和
系和 ![]() 系中的传播速度真的会都是
系中的传播速度真的会都是 ![]() 吗?没有任何东西能够在两个具有相对速度
吗?没有任何东西能够在两个具有相对速度 ![]() 的惯性系(
的惯性系( ![]() 系和
系和 ![]() 系)中,保持相同的速度。或者在
系)中,保持相同的速度。或者在 ![]() 系中的传播速度为
系中的传播速度为 ![]() ,在
,在 ![]() 系中则不为
系中则不为 ![]() ;或者在
;或者在 ![]() 系中速度为
系中速度为 ![]() ,在
,在 ![]() 系中则不为
系中则不为 ![]() ,不可能同时为
,不可能同时为 ![]() 。如果承认光速与光源速度无关(同子弹不一样),应该是后者。即光在静态空间
。如果承认光速与光源速度无关(同子弹不一样),应该是后者。即光在静态空间 ![]() 系中速度为
系中速度为 ![]() ,在
,在 ![]() 系中,射向车厢前端的光速为
系中,射向车厢前端的光速为 ![]() ,射向后端的光速为
,射向后端的光速为 ![]() 。这与在
。这与在 ![]() 系中,射向前后端的光与车厢的相对速度是相同的。因而,不管是在
系中,射向前后端的光与车厢的相对速度是相同的。因而,不管是在 ![]() 系中,还是在
系中,还是在 ![]() 系中观测,都是光先射到车厢的后壁,后射到车厢的前壁。
系中观测,都是光先射到车厢的后壁,后射到车厢的前壁。 ![]() 和
和 ![]() 两个事件不论是在
两个事件不论是在 ![]() 系或是在
系或是在 ![]() 系都不是同时的。
系都不是同时的。
子弹由车厢中间位置射向前后壁,将同时击中前后壁。光由中间位置射向前后壁,却不是同时达到的。区别在于子弹具有惯性,它的速度与发射体的速度有关,光的传播速度则与光源的速度无关。光在 ![]() 系中传播速度不能为
系中传播速度不能为 ![]() ,否则就像子弹一样,其传播速度与发射体(光源)的速度有关了。
,否则就像子弹一样,其传播速度与发射体(光源)的速度有关了。
2.5 洛仑兹速度转换和伽俐略转换
设 ![]() 坐标系相对
坐标系相对 ![]() 坐标系作匀速直线运动,速度为
坐标系作匀速直线运动,速度为 ![]() 。动点
。动点 ![]() 沿
沿 ![]() 速方向作直线运动,在
速方向作直线运动,在 ![]() 系中速度为
系中速度为 ![]() ,在
,在 ![]() 系中速度为
系中速度为 ![]() ,如图2.5-1所示。
,如图2.5-1所示。
按照洛仑兹速度转换关系,有
![]() 或
或 ![]()
按照伽俐略速度转换关系,为
![]() 或
或 ![]()
在众多的高校物理学教材中都有下述一个例题。
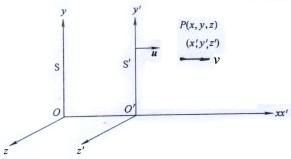
图2.5-1
设两飞船A和B分别以速度0.90c、-0.90c沿相反的方向相对地面水平飞行,求它们之间的相对速度,见图2.5-2。
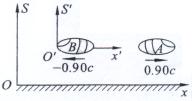
图2.5-2
在多数教材中,按洛仑兹速度转换公式计算。
设地面为 ![]() 系,飞船B为
系,飞船B为 ![]() 系,飞船A为运动体,其飞行方向为ox轴正向。
系,飞船A为运动体,其飞行方向为ox轴正向。
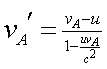
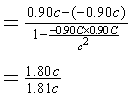
=0.994 ![]()
答案是两艘飞船之间的相对速度为0.944 ![]() 。
。
在康颖主编的《大学物理》(新版·科学出版社,2005年第1版,第1次印刷)中则指出:地面观测到飞船A相对于飞船B的速度,按伽俐略矢量合成法则计算为:
![]()
这就出现了两个相对速度:飞船A和B彼此观测时,相对速度为0.994 ![]() ;在地面观测时,它们之间的相对速度为1.80
;在地面观测时,它们之间的相对速度为1.80 ![]() 。
。
但是,两艘飞船之间真的会有两种相对速度吗?从地面观测也就是从整个物质体系的统一坐标系看,两艘飞船在1秒钟的时间内拉开的距离为54万公里,它们之间的相对速度为1.80 ![]() ,这是确定无疑的。让人们怀疑的是:两艘飞船相互观测时的相对速度真的为0.994
,这是确定无疑的。让人们怀疑的是:两艘飞船相互观测时的相对速度真的为0.994 ![]() 吗?从而也让人们怀疑洛仑兹速度转换的正确性。而洛仑兹转换是根据光速不变原理(光在所有惯性系中的传播速度都为
吗?从而也让人们怀疑洛仑兹速度转换的正确性。而洛仑兹转换是根据光速不变原理(光在所有惯性系中的传播速度都为 ![]() )推导出来的。对洛仑兹转换的质疑,再次让人们怀疑光速不变原理的正确性。
)推导出来的。对洛仑兹转换的质疑,再次让人们怀疑光速不变原理的正确性。
2.6 光速不变原理
光速在所有惯性系中的传播速率都等于恒量 ![]() ,它与光源,也与观测者的运动无关,称为光速不变原理。它是爱因斯坦狭义相对论的基础。
,它与光源,也与观测者的运动无关,称为光速不变原理。它是爱因斯坦狭义相对论的基础。
前面的几点讨论:两个平行运动体之间的光传播问题,爱因斯坦车厢光的前、后传播问题,两艘高速反向飞行的飞船之间的相对速度问题等,都导致对光速不变原理的怀疑。仅仅根据在地球(运动速度远低于光速)上进行的某些尚有争议的实验,就得到光速不变原理,这是欠慎重的。
下面再进行一些简单的分析。
两束迎面相射的光之间的相对速度是多少呢?按照狭义相对论,应该还是恒量 ![]() 。而从统一坐标系看,两束光之间每秒钟缩短的距离为60万公里,它们之间的相对速度是2倍光速
。而从统一坐标系看,两束光之间每秒钟缩短的距离为60万公里,它们之间的相对速度是2倍光速 ![]() 。从太阳发射出来的光,照到地球约8分钟。如果有一束光从太阳射向地球,同时又有一束光由地球射向太阳,4分钟后,两束光在太阳和地球之间的中间位置相遇。显然这两束光从射出到相遇,它们之间的相对速度不是光速
。从太阳发射出来的光,照到地球约8分钟。如果有一束光从太阳射向地球,同时又有一束光由地球射向太阳,4分钟后,两束光在太阳和地球之间的中间位置相遇。显然这两束光从射出到相遇,它们之间的相对速度不是光速 ![]() ,而是2倍光速
,而是2倍光速 ![]() 。也就是说,其中一束光在另一束光的坐标系中速度不是光速
。也就是说,其中一束光在另一束光的坐标系中速度不是光速 ![]() ,而是2倍光速
,而是2倍光速 ![]() 。也许这过于极端,光不能作为惯性系,我们可以把速度降低点:一束光在一个迎面而来、速率为0.5
。也许这过于极端,光不能作为惯性系,我们可以把速度降低点:一束光在一个迎面而来、速率为0.5 ![]() 的惯性系中速度为多少呢?难道还是光速
的惯性系中速度为多少呢?难道还是光速 ![]() ,而不是1.5
,而不是1.5 ![]() 吗?
吗?
如果有一前一后同向运行的两束光,它们之间的相对速度还是光速 ![]() 吗?从统一坐标
吗?从统一坐标
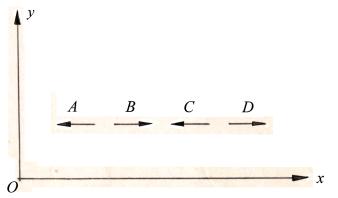
图2.6-1
系上看,它们之间前后的距离不变,相对速度应为0。也就是说,其中一束光在另一束光的坐标系中速度不为 ![]() ,而是0。也许这又过于极端,我们把速度降低一点。假设一束光在一个与之同向、速度为0.5
,而是0。也许这又过于极端,我们把速度降低一点。假设一束光在一个与之同向、速度为0.5 ![]() 的惯性系中传播,速度是多少呢?是
的惯性系中传播,速度是多少呢?是 ![]() 还是0.5
还是0.5 ![]() ?从统一坐标系看,应该是0.5
?从统一坐标系看,应该是0.5 ![]() ,而不是
,而不是 ![]() 。
。
请看图2.6-1。图中有4束光A、B、C、D。其中光波B和D沿 ![]() 轴正向运行,在光波B的后方和前方各有一束光波A和C,沿
轴正向运行,在光波B的后方和前方各有一束光波A和C,沿 ![]() 轴负向运行。按照狭义相对论,光波B和其它三束光A、C、D之间的相对速度均为
轴负向运行。按照狭义相对论,光波B和其它三束光A、C、D之间的相对速度均为 ![]() ,这显然是有问题的。从统一坐标系看,光波B和光波A之间是远离的2倍光速
,这显然是有问题的。从统一坐标系看,光波B和光波A之间是远离的2倍光速 ![]() ,光波B和光波C之间是趋近的2倍光速
,光波B和光波C之间是趋近的2倍光速 ![]() ,光波B和光波D之间的相对速度为0。
,光波B和光波D之间的相对速度为0。
2.7 迈克耳逊—莫雷实验
前面谈到,光速不变原理是根据在地球(运动速度远低于光速)上进行的某些尚有争议的实验推导出来的。这些实验中有著名的迈克耳逊—莫雷实验。迈克耳逊—莫雷实验的目的是观测地球相对以太(静态空间)的绝对运动。实验装置是迈克耳逊干涉仪。本文采用由赵近芳主编的《大学物理》(北京邮电大学出版社,2002年8月第1版,2002年11月第2次印刷)的叙述。
该仪器的光路原理如图2.7-1所示,实验原理说明如下。
设地球( ![]() 系)相对于太阳(
系)相对于太阳( ![]() 系)速度为
系)速度为 ![]() 。实验时,先将干涉仪的一臂(如
。实验时,先将干涉仪的一臂(如 ![]() )与地球运动方向(
)与地球运动方向( ![]() 速方向)平行。另一臂(如
速方向)平行。另一臂(如 ![]() )与地球运动方向(
)与地球运动方向( ![]() 速方向)垂直。根据伽俐略速度变换法则,在与地球固连的实验室坐标系中,光沿各方向传播的速度大小不相等。其中
速方向)垂直。根据伽俐略速度变换法则,在与地球固连的实验室坐标系中,光沿各方向传播的速度大小不相等。其中 ![]() 方向为(
方向为( ![]() )和
)和 ![]() ,
, ![]() 方向为
方向为 ![]() 和-
和- ![]() 。当两臂长度(
。当两臂长度( ![]() )相等时,光程差不为零,可以看到干涉条纹。如果将整个装置缓慢转过90°,应该发现干涉条纹移动。由条纹移动的数目,可以推算出地球相对以太(静态空间)参考系的绝对速度
)相等时,光程差不为零,可以看到干涉条纹。如果将整个装置缓慢转过90°,应该发现干涉条纹移动。由条纹移动的数目,可以推算出地球相对以太(静态空间)参考系的绝对速度 ![]() 。下面计算光线通过两臂往返的时间。
。下面计算光线通过两臂往返的时间。
光沿 ![]() 臂往返的时间为:
臂往返的时间为:
![]() (2.7-1)
(2.7-1)
光沿 ![]() 臂往返的时间为:
臂往返的时间为:
![]() (2.7-2)
(2.7-2)
时间差为:
![]() (2.7-3)
(2.7-3)
两臂转过90°后,时间差为:
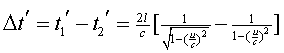 (2.7-4)
(2.7-4)
于是得到干涉仪转动前后,光通过两臂时间差的改变量为:
![]()
![]()
![]() (2.7-5)
(2.7-5)
考虑 ![]() 是小量,利用近似公式
是小量,利用近似公式
![]() ,
, ![]()
![]()
则 ![]()
应有干涉条纹移动的数目为
![]() (2.7-6)
(2.7-6)
式中 ![]() 是真空中光波的波长。
是真空中光波的波长。
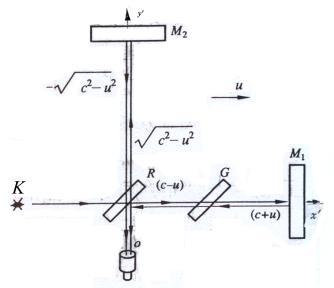 图2.7-1 图2.7-1 |
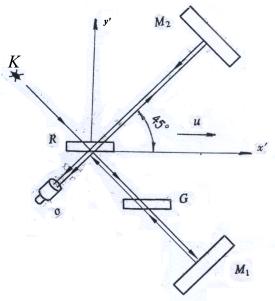 图2.7-2 图2.7-2 |
该教材说1891年迈克耳逊首次实验,没有观察到预期的条纹移动。1887年迈克耳逊和莫雷提高实验精度,使臂长 ![]() 米,光波长
米,光波长 ![]() 。如果取
。如果取 ![]() (为地球绕太阳公转的速度)预期
(为地球绕太阳公转的速度)预期 ![]() 条。但实验观测值小于0.01条。
条。但实验观测值小于0.01条。
问题出在哪里?我们先看几个图。
图2.7-1为干涉仪初始位置图。其中臂 ![]() 为
为 ![]() 方向,臂
方向,臂 ![]() 与
与 ![]() 方向垂直。
方向垂直。
图2.7-2为干涉仪两臂顺时针旋转45°位置,这时两臂相对于 ![]() 对称。
对称。
图2.7-3为干涉仪两臂自初始位置旋转90°的位置。臂 ![]() 为
为 ![]() 速方向,臂
速方向,臂 ![]() 与
与 ![]() 垂直。
垂直。
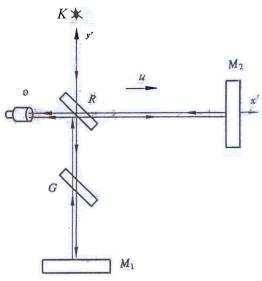 图2.7-3 图2.7-3 |
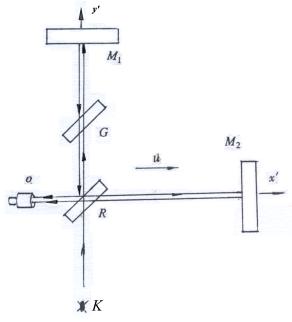 图2.7-4 图2.7-4 |
图2.7-4为干涉仪旋转90°后,再将臂 ![]() 绕臂
绕臂 ![]() 旋转180°的位置。其中臂
旋转180°的位置。其中臂 ![]() 为
为 ![]() 速方向,臂
速方向,臂 ![]() 与
与 ![]() 垂直,但不在
垂直,但不在 ![]() 方向的右侧(下侧),而是到了
方向的右侧(下侧),而是到了 ![]() 方向的左侧(上侧),即臂
方向的左侧(上侧),即臂 ![]() 的原初始位置。该图可视为干涉仪处于初始位置时两臂互换位置图。
的原初始位置。该图可视为干涉仪处于初始位置时两臂互换位置图。
参照上述几个图,我们进行一些分析。
一、图2.7-4和图2.7-3所示干涉仪两臂的光程差是相同的。只要臂 ![]() 与
与 ![]() 垂直,就不必考虑臂
垂直,就不必考虑臂 ![]() 是在
是在 ![]() 方向(臂
方向(臂 ![]() )的右侧(下侧)或是左侧(上侧)。
)的右侧(下侧)或是左侧(上侧)。
二、图2.7-4和图2.7-1相当于在初始位置,臂 ![]() 和臂
和臂 ![]() 互换位置。结合图2.7-3分析,干涉仪两臂旋转90°,即相当于两臂互换位置。
互换位置。结合图2.7-3分析,干涉仪两臂旋转90°,即相当于两臂互换位置。
三、干涉仪两臂旋转90°或是互换位置,对两臂的光程差有什么影响呢?
以往的分析认为干涉仪的两臂旋转90°,或是互换位置,其光程差数值不变,但正负号相反,旋转90°将导致光程差的改变量为原光程差的2倍。如图2.7-1所示,在初始位置,臂 ![]() 的光路比臂
的光路比臂 ![]() 的光路小一个光程差。
的光路小一个光程差。
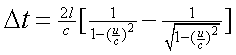
旋转90°后,臂 ![]() 的光路比臂
的光路比臂 ![]() 的光路大一个同样的光程差。因此在旋转过程中,臂
的光路大一个同样的光程差。因此在旋转过程中,臂 ![]() 和臂
和臂 ![]() 之间的光程差的改变量是原初始位置光程差的2倍。
之间的光程差的改变量是原初始位置光程差的2倍。
我们认为,两臂互换位置,光程差不仅数值相等,正负号也相同。两臂旋转90°时终止位置和起始位置的光程差改变量为零。
当两臂旋转90°或互换位置时,两臂的长度不变,其它条件(如透射、反射情况及两臂之间的夹角等)也相同,两臂的光程差应该是相同的(含正负号)。从干涉仪的制造和调试方面考虑,两臂各方面的光学条件都应该完全一样,否则就会影响数据,不能作为干涉仪使用。两臂的光程差,只与两臂同 ![]() 速之间的角度有关,而与臂的选择无关。只要两臂中,有一臂为
速之间的角度有关,而与臂的选择无关。只要两臂中,有一臂为 ![]() 速方向,另一臂与
速方向,另一臂与 ![]() 速方向垂直,就将有一个确定的光程差值,而不必考虑究竟是哪一个臂为
速方向垂直,就将有一个确定的光程差值,而不必考虑究竟是哪一个臂为 ![]() 速方向,哪一个臂与
速方向,哪一个臂与 ![]() 速方向垂直。因此,两臂互换位置,光程差不仅数值相等,正负号也相同。两臂旋转90°,光程差改变量为零。
速方向垂直。因此,两臂互换位置,光程差不仅数值相等,正负号也相同。两臂旋转90°,光程差改变量为零。
四、在两臂旋转90°的过程中,两臂的光程差有什么变化?
如图2.7-2所示,当两臂与 ![]() 方向成45°角时,光程差最小。从理论上讲,如两臂长度相等,这时两臂的光程差应为零。
方向成45°角时,光程差最小。从理论上讲,如两臂长度相等,这时两臂的光程差应为零。
由图2.7-1位置开始,两臂顺时针旋转,光程差逐渐减小,到图2.7-2位置(45°方向)光程差最小。
由图2.7-2位置继续顺时针旋转,两臂的光程差又逐渐加大。到图2.7-3位置,两臂的光程差与图2.7-1位置两臂的光程差相同。
由图2.7-1位置开始,两臂旋转90°,到图2.7-3位置的过程相当于由图2.7-1位置顺时针旋转45°,到图2.7-2位置,然后又逆时针旋转45°,回到图2.7-1位置。
五、如果取该教材提供的实验数据: ![]() 米,
米, ![]() ,
, ![]() ,由图2.7-1位置两臂旋转45°到图2.7-2位置,预期干涉条纹的移动数为0.185条。再由图2.7-2位置两臂旋转到图2.7-3位置,干涉条纹回移0.185条。终止位置(图2.7-3)和起始位置(图2.7-1)干涉条纹无变化。
,由图2.7-1位置两臂旋转45°到图2.7-2位置,预期干涉条纹的移动数为0.185条。再由图2.7-2位置两臂旋转到图2.7-3位置,干涉条纹回移0.185条。终止位置(图2.7-3)和起始位置(图2.7-1)干涉条纹无变化。
六、计算式(2.7-5)应该改一个正负号
![]() 应改为
应改为 ![]() ,即
,即
![]()
![]()
=0
七、利用迈克耳逊干涉仪观测地球相对静态空间的绝对运动应采用下述方法:
先将干涉仪的双臂置于与 ![]() 速成45°角度的方向,然后顺时针或逆时针将双臂旋转
速成45°角度的方向,然后顺时针或逆时针将双臂旋转
45°,使其中一臂为 ![]() 速方向,另一臂与
速方向,另一臂与 ![]() 速方向垂直,观测该过程中干涉条纹的移动。
速方向垂直,观测该过程中干涉条纹的移动。
第一篇结束语
自爱因斯坦提出狭义相对论,已有百余年,它早已为主流科学界所接受,被称为20世纪最重要的科学成果。然而,批评之声也从未间断过,人们一直怀疑狭义相对论的正确性。但是在大学的物理教材中,狭义相对论作为重要内容,一直在向学生讲授,却从不提及人们对它的批评,为了对青年学生负责,我们有责任向我们的学生提出狭义相对论的问题。
这些问题包括以下方面:
一、地球的运动速度较慢,在地球上进行的一些实验,包括迈克耳逊——莫雷的光波干涉实验,真能否定绝对空间的存在吗?
二、光速不变原理(光在任何惯性系中传播的速度均为 ![]() )真的正确吗?
)真的正确吗?
三、在高速运动时,真有洛仑兹转换吗?
四、所谓“动钟延缓”“同时的相对性”等概念对吗?
很遗憾,对于上述问题,我们均持否定态度。
如果迈克耳逊干涉仪的两臂具有相同的光学条件(两臂长度相等、透射、反射条件相同,两臂夹角保持不变等),当两臂旋转90°或交换位置时,两臂光程差的改变量应为零,而不是过去人们以为的是初始光程差的两倍。这个分析与实验结果相符。因此,迈克耳逊——莫雷光波干涉实验并不能否定绝对空间的存在,也不能证明光速不变原理。
狭义相对论认为,所有惯性系中测量到的真空中光速沿各个方向都等于 ![]() ,与光源的运动状态无关,称之为光速不变原理。也就是说光速与光源的运动状态无关,也与测量者的运动状态无关。我们认为,说“所有惯性系中测量到的真空中光速沿各个方向都等于
,与光源的运动状态无关,称之为光速不变原理。也就是说光速与光源的运动状态无关,也与测量者的运动状态无关。我们认为,说“所有惯性系中测量到的真空中光速沿各个方向都等于 ![]() ”,有点过于武断,因为人们至今只在地球惯性系中测量了光速,而地球的运动速度远低于光速。据此即认定“所有惯性系中测量到的真空中,光速沿各个方向都等于
”,有点过于武断,因为人们至今只在地球惯性系中测量了光速,而地球的运动速度远低于光速。据此即认定“所有惯性系中测量到的真空中,光速沿各个方向都等于 ![]() ”,显然欠妥。
”,显然欠妥。
按照基本的运动学常识,没有任何运动体,相对于两个速率不同的惯性系能保持同一速度。也没有任何运动体,在一个动态的惯性系中,能保持各个方向速度一致。光波只有在静态空间中,沿各个方向的传播速度才等于 ![]() ,而不会在所有惯性系中,沿各个方向都等于
,而不会在所有惯性系中,沿各个方向都等于 ![]() 。
。
光速不变原理的错误是显而易见的,明确它的错误将导致狭义相对论被全盘否定。根据光速不变原理推导出来的洛仑兹转换,“同时”的相对性,动钟延缓,动尺缩短等都将被否定。我们需要建立一种新的时空观。
迈克耳逊——莫雷实验并不能否定绝对空间的存在,事实上绝对空间是客观存在的,是否定不了的。巨大的,却仍是有限的物质存在于无限的静态空间中,并在其中运动、演变,这是我们的宇宙观。宇宙中所有的物质是一个整体,可称为物质世界或物质体系。整个物质体系具有统一的时间,它不会因运动者的速度快慢而改变,也不会因观测者的运动速度而改变。整个物质体系可以确定一个统一的中心坐标系统。在这样的涵盖整个物质体系的坐标系统中,任何物质点,在任何时刻都有确定的坐标位置,两个物质点之间的距离将不会因观测者的运动速度不同而改变,不会有动尺缩短的概念。在这样的统一坐标系中,只有伽俐略速度变换,而没有洛仑兹转换。同狭义相对论对立的是承继牛顿力学的、又有所发展的统一论:统一的物质体系、统一的坐标系、统一的时间。
第二篇 评哈勃定律
第三章 评哈勃定律
3.1 光谱线红移和哈勃定律
实验室内测定的某条光谱线波长为 ![]() ,观察者在地球测到某光源天体同一条谱线波长为
,观察者在地球测到某光源天体同一条谱线波长为 ![]() ,并设光源天体发射时该谱线波长为
,并设光源天体发射时该谱线波长为 ![]() ,一般认为
,一般认为 ![]() =
= ![]() 。
。
光源天体光谱线波长的改变量为 ![]() ,有
,有 ![]() =
= ![]() ,或
,或 ![]() 。
。
波长改变量 ![]() 和波长
和波长 ![]() 的商称为光谱线移动量,以Z表示
的商称为光谱线移动量,以Z表示
![]()
或 ![]()
![]() 增加,谱线向红光端移动称为红移;
增加,谱线向红光端移动称为红移; ![]() 减小,谱线向紫光端移动,称为紫移。在天文观测中,天体的光谱线多为红移。
减小,谱线向紫光端移动,称为紫移。在天文观测中,天体的光谱线多为红移。
根据多普勒原理红移说明光源天体远离我们地球,红移量Z等于光源天体和观测者的视线速度 ![]() 和光速C的商。
和光速C的商。
![]() 或
或 ![]() =Z·C
=Z·C
![]() 又称退行速度。
又称退行速度。
1929年美国天文学家哈勃确定河外星系的谱线红移值Z和它们到地球的距离r成正比,由此又确定视线速度 ![]() 和r成正比。
和r成正比。
![]() 或
或 ![]()
这就是著名的哈勃定律。其中H表示视线速度 ![]() 和距离r的商,确定为一个常数,称哈勃常数。
和距离r的商,确定为一个常数,称哈勃常数。
该定律认为谱线红移即为距离红移 ![]() (与距离r成正比的红移),也就是视线速度红移
(与距离r成正比的红移),也就是视线速度红移 ![]() (与视线速度
(与视线速度 ![]() 成正比的红移)。并且,根据这种认识推断,视线速度
成正比的红移)。并且,根据这种认识推断,视线速度 ![]() 和距离 r成正比。
和距离 r成正比。
3.2 问题
3.2.1 哈勃常数是常数吗?
数十年来,哈勃常数的数值一直难以确定,由超过500千米/百万秒差距·秒,到50千米/百万秒差距·秒,反复不定。令人怀疑,究竟是难以准确测量,还是因为哈勃常数原本就不是常数,即视线速度 ![]() 与距离r不成正比。
与距离r不成正比。
3.2.2 产生光谱线红移的原因是多普勒效应吗?
经验告诉我们声波的多普勒效应只在近距离有效,当超过一定距离后多谱勒效应并不明显,见图3.2-1。图中横坐标为距离 ![]() ,纵坐标为声波的频率
,纵坐标为声波的频率 ![]() ,测量者的位置在坐标原点O,声源体以
,测量者的位置在坐标原点O,声源体以 ![]() 速向右运动。在声源体靠近时,测量者测得声波频率急剧升高;当声源体越过测量者远离时,测量者测得声波频率急剧下降。但在距离较远处,不论是趋近,还是远离,声波频率无明显的变化。
速向右运动。在声源体靠近时,测量者测得声波频率急剧升高;当声源体越过测量者远离时,测量者测得声波频率急剧下降。但在距离较远处,不论是趋近,还是远离,声波频率无明显的变化。
声波的多普勒效应只在近距离内有效,如果在光波方面也是这样的话,哈勃定律将被否定,远距离的光谱线红移将不会是多普勒效应。
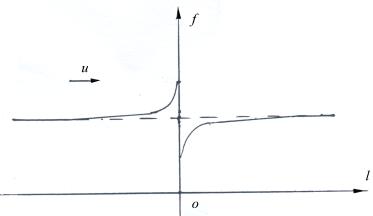
图3.2-1
3.2.3 星体谱线的大红移值否定公式 ![]() 。
。
随着天文观测的发展,天文学家发现了一些谱线红移值特别大的星体,其中一些星体谱线红移值Z超过了4。按照公式 ![]() ,这些星体和银河系的视线速度应该是光速的4倍以上。根据相对运动原理,视线速度超过了光速,我们将不可能见到该星体发出的光。
,这些星体和银河系的视线速度应该是光速的4倍以上。根据相对运动原理,视线速度超过了光速,我们将不可能见到该星体发出的光。
星体谱线的大红移值,否定了公式 ![]() 。红移值不能等于视线速度
。红移值不能等于视线速度 ![]() 和光速c的商。
和光速c的商。
3.3 什么情况下视线速度能与距离成正比?
哈勃定律认为视线速度 ![]() 和距离r成正比。二者之商是一个常数,称哈勃常数,即
和距离r成正比。二者之商是一个常数,称哈勃常数,即 ![]() ,那么在什么情况下,视线速度
,那么在什么情况下,视线速度 ![]() 能与距离r成正比呢?
能与距离r成正比呢?
3.3.1 一维膨胀模型
学者们常用宇宙膨胀理论解释哈勃定律。在保尔戴维斯著的《宇宙的最后三分钟》(上海科学出版社.1999年)中,作者引入一维膨胀模型,见图3.3.1-1。该图以钮扣代表星系,橡皮带代表空间。橡皮带伸长时钮扣彼此远离。钮扣离得越远,它退行得越快,这种膨胀意味着退行速率与距离成正比。同时伸长的作用使沿橡皮带传播的波的波长变长,以此解释宇宙学红移现象。
但是,宇宙中星系的扩散(“宇宙膨胀”)显然不会是这种一维模型。
3.3.2 引入星系均衡扩散(“宇宙均衡膨胀”)的球面模型。
假如宇宙中各个星系以相等的速度向外扩散(或称“宇宙均衡膨胀”),星系将分布在一个球面上。这种星系呈球面向外扩散的模型,也许是唯一个能解释视线速度 ![]() 与距离r成正比的三维模型,那么我们看看在这种三维球面模型中,星系的观测位置与星系扩散速
与距离r成正比的三维模型,那么我们看看在这种三维球面模型中,星系的观测位置与星系扩散速
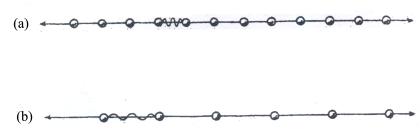
图3.3.1-1
度之间的关系。从这种应该有的星系观测位置,判断宇宙中的星系真的是按球面状态扩散的吗?如果是,视线速度尚有可能与距离成正比,如果不是,则视线速度便不可能与距离成正比?哈勃定律难以成立。
3.4 星系均衡扩散的三维球面模型
3.4.1 三维球面模型
假设星系均衡向外扩散,星系分布在一个球面上。设星系的扩散速度为 ![]() ,扩散时间为T(即所谓宇宙年龄)。星系分布的球面半径为R,
,扩散时间为T(即所谓宇宙年龄)。星系分布的球面半径为R, ![]() ,球面中心为O。
,球面中心为O。
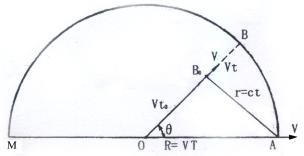
图3.4.1-1
设银河系的位置在A,另一个星系现在在球面的B位置。我们观测到的该星系发射来的光却不是该星系在B处发来的,而是该星系t时间前在 ![]() 处发射来的光。由
处发射来的光。由 ![]() 到A的距离为r,有
到A的距离为r,有 ![]() ,c为光速。A、B两星系扩散时的距离、速度和时间之间的关系,请参看图3.4.1-1。其中A、B两星系间扩散方向(扩散半径)之间的夹角为
,c为光速。A、B两星系扩散时的距离、速度和时间之间的关系,请参看图3.4.1-1。其中A、B两星系间扩散方向(扩散半径)之间的夹角为 ![]() 。星系B在
。星系B在 ![]() 位置时的扩散时间为
位置时的扩散时间为 ![]() ,由
,由 ![]() 再经过t时间到达现在的球面位置B,
再经过t时间到达现在的球面位置B, ![]() 。
。
3.4.2 三维球面模型分析
参看图3.4.1.-1,在三角形 ![]() 中,根据余弦定理,有
中,根据余弦定理,有
![]()
![]()
把 ![]() 代入\\
代入\\
![]()
化简: ![]()
解得: 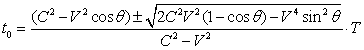
取负数根号 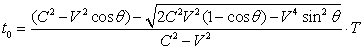
设K=V/C即V=KC,其中 ![]()
![]()
上述结果表明,当星系扩散速度V等于某一个值时,时间 ![]() 和角度
和角度 ![]() 之间存在一定的函数关系。
之间存在一定的函数关系。
令 ![]()
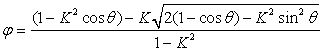
在下述表3.4.2-1中列出了K分别等于0.05,0.1,0.3,0.5,0.8,0.9时各个角度 ![]() 所对应的
所对应的 ![]() 值。
值。
表3.4.2-1 各种扩散速度对应的 ![]() 值
值
|
K |
0° |
5° |
15° |
30° |
45° |
60° |
75° |
90° |
105° |
120° |
135° |
150° |
165° |
180° |
|
0.9 |
1 |
0.8363 |
0.5863 |
0.3589 |
0.2342 |
0.1642 |
0.1221 |
0.0958 |
0.0789 |
0.0679 |
0.0610 |
0.0563 |
0.0537 |
0.0526 |
|
0.8 |
1 |
0.8889 |
0.7069 |
0.5081 |
0.3753 |
0.2864 |
0.2269 |
0.1861 |
0.1583 |
0.1389 |
0.1258 |
0.1172 |
0.1125 |
0.1111 |
|
0.5 |
1 |
0.9515 |
0.8599 |
0.7424 |
0.6451 |
0.5657 |
0.5020 |
0.4515 |
0.4120 |
0.3820 |
0.3600 |
0.3449 |
0.3363 |
0.3333 |
|
0.3 |
1 |
0.9730 |
0.9211 |
0.8500 |
0.7866 |
0.7311 |
0.6834 |
0.6433 |
0.6102 |
0.5838 |
0.5644 |
0.5496 |
0.5412 |
0.5385 |
|
0.1 |
1 |
0.9899 |
0.9735 |
0.9488 |
0.9260 |
0.9045 |
0.8851 |
0.8676 |
0.8527 |
0.8405 |
0.8310 |
0.8238 |
0.8197 |
0.8182 |
|
0.05 |
1 |
0.9956 |
0.9870 |
0.9744 |
0.9624 |
0.9512 |
0.9409 |
0.9317 |
0.9237 |
0.9170 |
0.9117 |
0.9079 |
0.9055 |
0.9048 |
3.4.3 星系均衡扩散时星系观测位置与扩散速度的关系
图3.4.3-1绘出了K分别等于0.05,0.1,0.3,0.5,0.8,0.9时所对应的星系观测位置曲线。该图绘的是球面过中心的圆剖面图,且只绘了半个圆。把各曲线绕MOA轴(直径)旋转一周,即可获得各星系在空间的观测位置曲面图。该图的一个重要特征是:所有的星系将在银河系的一侧。
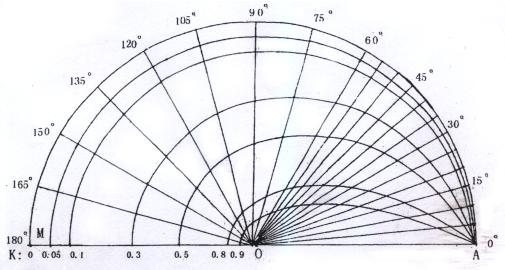
图3.4.3-1
在星空实际的观测中,星系是按这样的曲面分布的吗?如果是,星系将是均衡按球面模型扩散的;如果不是,则星系将不是均衡地按球面模型扩散的。目前的天文观测尚无法确定宇宙中所有的星系是否分布在这样的曲面上,无法证明星系是均衡地按球面模型扩散的。如果星系按球面模型均衡扩散的方式被否定,意味着视线距离 ![]() 难以与距离r成正比,
难以与距离r成正比, ![]() 常数,哈勃定律难以成立。
常数,哈勃定律难以成立。
3.5 谱线红移的其它解释
3.5.1 宇宙膨胀理论
有人提出宇宙膨胀的理论解释谱线红移,用空间尺度的扩大解释红移。该理论认为所谓红移指的是观测到的天体光源波长 ![]() 和发射时的波长
和发射时的波长 ![]() 相比较。在宇宙膨胀的情况下,发射时刻
相比较。在宇宙膨胀的情况下,发射时刻 ![]() 的空间尺度
的空间尺度 ![]() 与现在观测时刻t的空间尺度
与现在观测时刻t的空间尺度 ![]() 是不同的,波长也会随着空间尺度的变化(放大)而变化(放大)。相应有:
是不同的,波长也会随着空间尺度的变化(放大)而变化(放大)。相应有:
![]()
红移可表示为:
![]()
红移的实质就是波长随着空间尺度的膨胀而自然增长。观测得越远,所代表的宇宙年龄越早,红移也越大。
初看起来这种理论颇有道理,似乎完美地解释了红移现象。但是,仔细分析,这种宇宙膨胀理论不仅不能解释红移现象,反倒让人怀疑宇宙膨胀理论的正确性。
如前面所言,我们谈到了一种谱线的三种波长:即实验室光源某条谱线的波长为 ![]() ,星体光源发射时该种谱线的波长
,星体光源发射时该种谱线的波长 ![]() 和地球观测到的星体光源谱线的波长
和地球观测到的星体光源谱线的波长 ![]() 。并且我们定义红移为:
。并且我们定义红移为:
![]()
即:地球观测到的星体光源谱线波长 ![]() 和实验室光源同种谱线波长
和实验室光源同种谱线波长 ![]() 的差,同实验室光源波长
的差,同实验室光源波长 ![]() 的商。
的商。
该理论错误之处是在公式中用 ![]() 代替了
代替了 ![]() ,即认为星体光源发射时谱线的波长
,即认为星体光源发射时谱线的波长 ![]() 即实验室光源谱线波长
即实验室光源谱线波长 ![]() 。
。
如果不存在宇宙膨胀的影响,即过去的空间尺度 ![]() 和现在的空间尺度
和现在的空间尺度 ![]() 相同,这时
相同,这时 ![]() =
= ![]() ,这种替换是可以的。
,这种替换是可以的。
有 ![]()
如果存在宇宙膨胀的影响,过去的空间尺度 ![]() 不等于现在的空间尺度
不等于现在的空间尺度 ![]() 。星体光源在过去空间尺度
。星体光源在过去空间尺度 ![]() 下的波长
下的波长 ![]() 与现在空间尺度
与现在空间尺度 ![]() 下实验室光源谱线波长
下实验室光源谱线波长 ![]() 并不相等,即
并不相等,即 ![]() ≠
≠ ![]() ,因此
,因此
![]() ≠(
≠( ![]() -
- ![]() )/
)/ ![]()
我们定义红移时,用的波长 ![]() 和
和 ![]() 都是现在空间尺度
都是现在空间尺度 ![]() 下谱线的波长,而不是用过去空间尺度
下谱线的波长,而不是用过去空间尺度 ![]() 下的波长
下的波长 ![]() ,我们所定义的红移并不考虑空间尺度的变化。
,我们所定义的红移并不考虑空间尺度的变化。
如果考虑空间尺度的扩大,有 ![]() <
< ![]()
则: ![]()
这表示考虑宇宙膨胀影响的红移值 ![]() 将大于我们所定义的红移值
将大于我们所定义的红移值 ![]() 。或者说,在我们所定义的红移值
。或者说,在我们所定义的红移值 ![]() 中不包含宇宙膨胀,即空间尺度扩大的影响,而是另有其他的影响因素。
中不包含宇宙膨胀,即空间尺度扩大的影响,而是另有其他的影响因素。
如果只存在宇宙膨胀的影响因素,而无其他影响因素,天体光源在过去空间尺度 ![]() 下发射出的波长为
下发射出的波长为 ![]() 的光谱线,随着宇宙的膨胀,空间尺度的扩大,波长自然增加到了
的光谱线,随着宇宙的膨胀,空间尺度的扩大,波长自然增加到了 ![]() ,这时的波长
,这时的波长 ![]() 应与同为现在空间尺度下实验室光源谱线波长
应与同为现在空间尺度下实验室光源谱线波长 ![]() 相等,有
相等,有 ![]()
![]() =0
=0
此时红移值为零。
再次说明宇宙膨胀,即空间尺度的扩大不是产生红移的原因,用宇宙膨胀的理论,不能解释我们所说的红移现象。
3.5.2 引力红移
为了解释大红移值问题,有学者提出了引力红移的概念。
按照广义相对论,处在引力场中的辐射源发出的光,当从远离引力场的地方观测时,谱线会向长波方向移动,移动量与光源和观测者两处引力势差的大小成正比,光谱线的这种红移称为引力红移。不过这种红移值很小,要造成巨大红移3或4,需要质量非常巨大(一亿个太阳质量)的黑洞。在这种强引力场中,谱线将会很宽,而与实际观测到的大红移星体的谱线宽度不符,引力红移也难以解释星体谱线的大红移。
3.6 产生红移的原因是光子能量的衰减
3.6.1 谱线红移是光子能量的自然衰减
根据量子理论,光子的能量 ![]() ,其中f 是光的频率,h为普朗克常量。设光源天体发射时光子能量为
,其中f 是光的频率,h为普朗克常量。设光源天体发射时光子能量为 ![]() ,频率为
,频率为 ![]() ,波长为
,波长为 ![]() 。地球观测者,测到的光子能量为E,频率为f,波长为
。地球观测者,测到的光子能量为E,频率为f,波长为 ![]() 。
。
红移值 ![]()
= ![]()
= ![]()
波长的变化表示光子能量的变化,红移表示光子能量的衰减。
光波在长距离(长时间)的传播过程,即光子在长距离(长时间)的运动过程中能量的自然衰减是产生谱线红移的主要的原因,产生谱线红移的主要原因不是多普勒效应。
哈勃确定河外星系的谱线红移值Z和它们到地球的距离r成正比,这是正确的。但是用多普勒效应解释谱线红移则错了。
3.6.2 能量衰减理论的意义
一旦确定光子能量的自然衰减是产生谱线红移的主要原因,这将给现代天文学带来一些新的影响。
星体谱线红移值的测定将帮我们简单、准确地测量该星体到地球的距离。红移值Z与距离成正比,即 ![]() ,其中
,其中 ![]() 为红移的距离系数,确定了
为红移的距离系数,确定了 ![]() 我们就能很方便地测量星系和地球之间的距离了。
我们就能很方便地测量星系和地球之间的距离了。
产生谱线红移的原因如果不是多普勒效应,将对星系扩散(“宇宙膨胀”)的理论带来致命的影响。过去认为,谱线红移表明星体在远离我们而去,而且距离越远的星体,退行速度越大,从而说明星系是朝外扩散(“宇宙膨胀”)的。如果认定产生谱线红移的原因并非多普勒效应,那么谱线红移与视线速度无关。谱线红移不能证明星体在远离我们,不能证明星系是朝外扩散的(“宇宙膨胀”),“宇宙膨胀”理论将需要重新考虑。
第二篇结束语
1929年,美国天文学家哈勃确定河外星系的谱线红移Z和它们到球的距离r成正比。但是却错误的认为产生谱线红移的原因是多普勒效应,从而确定视线速度 ![]() 和距离r成正比,有
和距离r成正比,有 ![]() ,提出了著名的哈勃定律。其中H为视线速度
,提出了著名的哈勃定律。其中H为视线速度 ![]() 和距离r的商,称为哈勃常数。
和距离r的商,称为哈勃常数。
哈勃定律的怀疑者提出产生谱线红移的原因并非多普勒效应,声波的多普勒效应只在近距离显剧,而在较远的距离多普勒效应不明显,如果光波也是这样,那么远距离的红移将不会是多普勒效应。此外,多普勒效应也无法解释大红移值问题。
视线速度 ![]() 真的与距离r成正比吗?数十年来,人们无法精确地测定哈勃常数,让人怀疑哈勃常数真为常数吗?只有星系均衡扩散(“宇宙均衡膨胀”)的三维球面模型能解释视线速度
真的与距离r成正比吗?数十年来,人们无法精确地测定哈勃常数,让人怀疑哈勃常数真为常数吗?只有星系均衡扩散(“宇宙均衡膨胀”)的三维球面模型能解释视线速度 ![]() 与距离r成正比,这种三维球面模型中的星系观测位置是一种特定的,与扩散速度有关的曲面,目前的天文观测尚无法确定宇宙中所有的星系是否分布在这样的曲面上。
与距离r成正比,这种三维球面模型中的星系观测位置是一种特定的,与扩散速度有关的曲面,目前的天文观测尚无法确定宇宙中所有的星系是否分布在这样的曲面上。
产生谱线红移的主要原因不是光波的多普勒效应,而是光子在运动过程中能量的自然衰减。
![]()
= ![]()
其中 ![]() 为光源天体发射光子的能量,E为地球上测到的光子能量。
为光源天体发射光子的能量,E为地球上测到的光子能量。
谱线红移值Z与距离r成正比,即 ![]() ,其中
,其中 ![]() 为红移的距离系数,也就是光子在长距离(长时间)的传播过程中的能量衰减系数。
为红移的距离系数,也就是光子在长距离(长时间)的传播过程中的能量衰减系数。
确定了谱线红移的距离系数(光子能量的衰减系数)我们将能利用谱线红移简单精确地测定星系到地球的距离。
当确定了产生谱线红移的主要原因不是光波的多普勒效应后,星系朝外扩散(“宇宙膨胀”)的理论将需要重新考虑。
2011年7月完稿
参考文献
(1) 《科学的丰碑—20世纪重大科技成就纵览》陈建礼主编,山东科学出版社,1998年。
(2) 《大学物理手册》胡盘新主编,上海交大出版社,1999年。
(3) 《宇宙—物理学的最大研究对象》陆士炎著,湖南教育出版社,1999年。
(4) 《爱因斯坦是怎样创建相对论的》尤广建著,湖南教育出版社,1999年。
(5) 《宇宙的最后三分钟》保尔·戴维斯著,傅承启译,上海科学出版社,1999年。
(6) 《相对论的意义》阿尔伯特·爱因斯坦著,上海科学教育出版社,2003年。
(7) 《空间、时间和引力》王永久著,湖南教育出版社,1999年4月笫1版笫4次印刷。
(8) 《大学物理》康颖主编,新版,科学出版社,2005年第1版第1次印刷。
(9) 《大学物理》赵近芳主编,北京邮电大学出版社,2002年11月第1版笫2次印刷。
作者简介
周君毅 湖南省株洲市人,1944年6月出生。1967年毕业于中南矿冶学院(現为中南大学)探矿工程专业。后赴青海省冶金地质七队工作。于1979年调回株洲市湖南冶金工业学校(现并入湖南工业大学)任教,讲授工程力学。编有《工程力学》教材。創建了利用隨荷载升降法绘制剪力图、利用剪力图面积连加法求控制截面弯矩的“绘制弯矩图的简捷法”。该方法在工程力学教学中获得了广泛的应用。退休前技术职称为机械专业副教授。
